Fitting the FIRC Model, and estimating variation in intervention impact across sites, in R
by Luke MiratrixWhen estimating average treatment impact for a multisite randomized trial, recent literature (see Bloom et al. (2017)) has suggested using the so-called FIRC (Fixed Intercept, Random Coefficient) model. There are some technical details that make fitting this model slightly tricky in R; this post talks through these details and also provides some code to fit this model.
The model is, for student \(i\) in site \(j\):
\[ \begin{aligned} Y_{ij} &= \alpha_{j} + \beta_j Z_{ij} + \epsilon_{ij} \\ & \qquad \epsilon_{ij} \sim N( 0, \sigma^2_z ) \mbox{ for } z = 0, 1 \\ \alpha_{j} &= \alpha_j \\ \beta_{j} &= \tau + u_{j} \\ & \qquad u_{j} \sim N( 0, \tau^2 ) \end{aligned} \]
In this model, each site has its own Average Treatment Effect (ATE), \(\beta_j\), and we model these ATEs using a random effect for the slope. The “FI” part is that we have a fixed effect for each site, rather than having the intercept also be a random effect. This solves a bunch of problems, in particular the problem of what happens if the sites have varying proportions of units treated. (If all sites have the same proportion of units treated, then you can pretty much do what you want and it won’t matter.)
The other secret sauce element of FIRC is the treatment-group-specific residual error variance. If the effect of an intervention varies within site (as is often the case), the treatment and control groups can have different within-site outcome variances. Allowing the residual error variance (\(Var( \epsilon_{ij})\)) to be different for treatment and control groups aims to account for this, avoiding model misspecification.
Fitting this model provides two nice pieces of information: an overall ATE estimate and an estimate of cross-site impact variation (both with standard errors). You can also use it to get partially pooled (i.e., shrunken, or stabilized) estimates of the average treatment effects for each site.
The FIRC model is estimating a superpopulation site-average effect, sort of, as discussed in Miratrix, Weiss, and Henderson (2021). In brief (and see Miratrix, Weiss, and Henderson (2021) for more on this), the FIRC model does not give an unbiased estimate for the site-average effect, and will tend towards a precision-averaged effect when there is less cross-site variation detected. This means, in a situation where the size of the site correlates with the intervention’s impact in the site, the FIRC model will estimate something between the average impact of the intervention weighting each site equally and the average impact of the intervention weighting each site by its sample size.
Fitting the FIRC model in R
The easiest way to fit the FIRC model, according to me, is to use the blkvar package that is a product of my CARES Lab.
To install this package you need to install it off GitHub as so:
install.packages("devtools")
devtools::install_github("https://github.com/lmiratrix/blkvar")
library( blkvar )A test dataset
To illustrate its use, first we generate some fake data (with an ATE of 0.3 and a cross site impact variation of \(0.2^2\)), also using the package:
set.seed(49497)
dat = generate_multilevel_data( n.bar = 70, J = 30,
variable.p = TRUE,
size.impact.correlate = 1,
zero.corr = TRUE,
ICC = 0.15,
gamma.10 = 0.3,
tau.11.star = 0.2^2 )
dat$X = dat$Y0 + rnorm( nrow(dat), sd = 2 )We have added a predictive covariate, \(X\), to illustrate adding in controls as well.
The larger sites in our data have larger impacts (due to size.impact.correlate), and the average intercept of the site is not correlated with the average impact of the site.
See the technical appendix B of Miratrix, Weiss, and Henderson (2021) posted here.
We can see how our site level ATEs vary by site size, just to prove we have some data:
library( tidyverse )
sdat <- dat %>% group_by( sid ) %>%
summarise( beta = mean(Y1 - Y0),
n = n() )
ggplot( sdat, aes( n, beta ) ) +
geom_point()
Fitting the model
We can analyze data with a single call to estimate_ATE_FIRC(), where we give the outcome, treatment assignment (as a 0/1 vector) and site indicator.
We can also add control variables using the formula notation of “~ X1 + X2 + ....”
The estimate_ATE_FIRC() method will then fit the multilevel model and return a few key results:
res = estimate_ATE_FIRC( Yobs, Z, sid, data=dat,
control_formula = ~ X)
res## Cross-site FIRC analysis (REML)
## Grand ATE: 0.3701 (0.06423)
## Cross-site SD: 0.2466 (0.03187)
## deviance = NA, p=NAThe “Grande ATE” is the estimated average impact across sites (subject to the precision-weighting caveats above), and the “Cross-site SD” is the estimate of cross-site impact variation from the FIRC model.
The default of estimate_ATE_FIRC() is to use restricted maximum likelihood (REML) for estimation, which we highly recommend.
If you want to test for whether there is impact variation, proponents of FIRC suggest, in Weiss et al. (2017), that one is better off testing for cross-site impact heterogeneity with a \(Q\)-statistic meta analytic approach of:
analysis_Qstatistic( Yobs, Z, sid, data=dat, calc_CI = TRUE )## Cross-site Q-statistic analysis
## Grand ATE: 0.3993
## Cross-site SD: 0.291 (90% CI 0.1896--0.4554)
## Q = 68.08, p=0.0001
## [ tolerance = 1e-05; mean method = weighted; est method = MoM ]The Grand ATE is the precision weighted average of site impacts. The Cross-site SD is again the estimated cross site variation, here estimated using the method of moments technique described by Konstantopoulos in Chapter 11 of Teo (2014). The confidence interval is for the amount of cross site variation. Importantly, this is a different estimation strategy than FIRC.
Why not use FIRC for testing?
To test for impact variation with FIRC, you would probably use a likelihood ratio test, comparing the model with a random effect for impact to one without. You can get this by specifying testing as follows:
res2 = estimate_ATE_FIRC( Yobs, Z, sid, data=dat,
include_testing = TRUE,
control_formula = ~ X)
res2## Cross-site FIRC analysis (ML)
## Grand ATE: 0.3987 (0.04091)
## Cross-site SD: 0.01144 (0.001052)
## deviance = -0.03386, p=0.5000To use a likelihood ratio test, you are forced to use maximum likelhood, not REML.
Unfortunately, simple ML can be badly biased in the face of moderate impact heterogeneity; see the very small estimate for impact heterogeniety above.
The blkvar package allows a REML=TRUE (or FALSE) to control which method to use; if you don’t specify, then it will pick depending on whether include_testing=TRUE (or FALSE), defaulting to REML when it can.
Overall, for testing, the Q-Statistic is preferred. That being said, the Q-statistic approach, as implemented here, unfortunately does not allow for the incorporation of the covariates; this is something for future work!
Getting the Empirical Bayes estimates
One nice thing about using a multilevel model such as the FIRC model is you can get empirical Bayes (shrunken) site-specific estimates for the site-average impacts.
You can use the blkvar package to get a tibble of these estimates:
site_ates = get_EB_estimates( res )
print( site_ates, n = 4 )## # A tibble: 30 × 2
## sid beta_hat
## <chr> <dbl>
## 1 1 0.456
## 2 2 0.323
## 3 3 0.432
## 4 4 0.0893
## # ℹ 26 more rowsFor kicks, we can compare our estimates to the truth, since we have synthetic data:
site_ates = left_join( site_ates, sdat, by="sid" )
ggplot( site_ates, aes( beta, beta_hat ) ) +
geom_point() +
labs( x = "True ATE", y = "EB estimated ATE" ) +
geom_abline( intercept = 0, slope = 1 ) +
coord_fixed()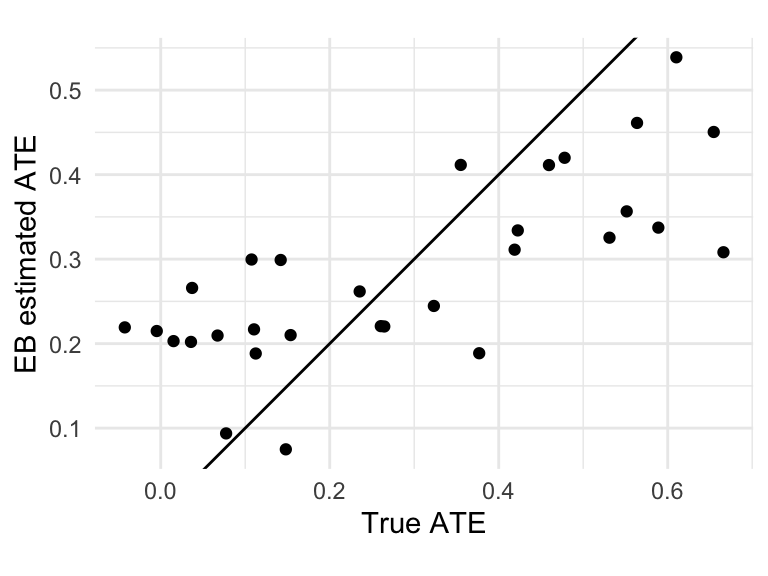
Unpacking the code
So what is the blkvar package doing? How do you really fit FIRC in R without an annoying and unverified package?
Well, the critical R code is the following:
re.mod <- nlme::lme( Yobs ~ 0 + Z + X + sid,
data = dat,
random = ~ 0 + Z | sid,
weights = nlme::varIdent(form = ~ 1 | Z),
na.action=stats::na.exclude, method = "REML",
control=nlme::lmeControl(opt="optim",returnObject=TRUE))The first line is the fixed part of the model. The sid makes all the site dummy variables. Z is our treatment and X is our covariate we made for illustration.
The “0 +” means no grand intercept; we instead have an intercept for each site via the sid dummy variables.
The third line makes the coefficient of Z a random effect, one for each group defined by sid (listed to the right of the “|”), and the “0 +” specifies no random intercept.
The nlme::varIdent(form = ~ 1 | Z) portion is what gives each stratum, defined by treatment group, its own variance parameter.
For those interested, the “0 +” notation bears a bit of further commentary: R likes to add grand intercepts by default. If there were no “0 +” in the first place, then one of the site dummies would be dropped, making that group the reference group, and the others would be relative to that group.
This would not actually impact the estimated treatment impact or random slope terms in this case.
If there were no “0 +” in the second place, R would automatically allow a random intercept for each site (which would break in our case since we also had fixed effects).
We are fitting using Restricted Maximum Likelihood; the default is to use ML to allow for a likelihood ratio test for the variance parameter (this test is part of the printout in the estimate_ATE_FIRC method, above).
REML, for FIRC models, gives much better estimates for cross-site impact variation.
Use REML here, and use the Q-statistic approach for testing rather than a likelihood ratio test on the fit FIRC model.
We can pull out the estimated grand ATE and associated standard error as follows:
# ATE
nlme::fixef(re.mod)[[1]]## [1] 0.3701# Estimated SE for the ATE
sqrt(vcov(re.mod)[1, 1])## [1] 0.06423We can pull out the estimated variation in impacts (\(\tau^2\)) as so:
VarCorr(re.mod)## sid = pdLogChol(0 + Z)
## Variance StdDev
## Z 0.06082 0.2466
## Residual 0.69622 0.8344To get a printout of the full model fit, do the following:
print( re.mod )## Linear mixed-effects model fit by REML
## Data: dat
## Log-restricted-likelihood: -2658
## Fixed: Yobs ~ 0 + Z + X + sid
## Z X sid1 sid2 sid3 sid4 sid5 sid6
## 0.37010 0.18371 -0.02277 -0.16652 -0.13749 -0.20470 -0.76809 0.14019
## sid7 sid8 sid9 sid10 sid11 sid12 sid13 sid14
## -0.52918 -0.43519 -0.18856 0.16931 0.82170 0.71641 -0.34780 -0.14498
## sid15 sid16 sid17 sid18 sid19 sid20 sid21 sid22
## -0.02905 0.12295 -0.49748 -0.01375 0.39273 0.31910 -0.24059 0.19465
## sid23 sid24 sid25 sid26 sid27 sid28 sid29 sid30
## -0.03964 -0.18624 -0.05648 0.41457 0.06110 -0.26630 0.30019 0.28689
##
## Random effects:
## Formula: ~0 + Z | sid
## Z Residual
## StdDev: 0.2466 0.8344
##
## Variance function:
## Structure: Different standard deviations per stratum
## Formula: ~1 | Z
## Parameter estimates:
## 1 0
## 1.0000 0.9976
## Number of Observations: 2117
## Number of Groups: 30The “Parameter estimates” part of the output shows the estimates for residual variance as scalings to the residual term.
The first group will have a scaling of 1.0 (no scaling), making the second number the relative variance.
So the control has an estimated variance about the same as the treatment group.
You can also use summary(), but the output gets messy with all the fixed effects for site. You can remove them, if you are crafty:
s = summary( re.mod )
s$tTable = s$tTable[1:2,]
s$corFixed = s$corFixed[1:2, 1:2]
print( s )## Linear mixed-effects model fit by REML
## Data: dat
## AIC BIC logLik
## 5386 5583 -2658
##
## Random effects:
## Formula: ~0 + Z | sid
## Z Residual
## StdDev: 0.2466 0.8344
##
## Variance function:
## Structure: Different standard deviations per stratum
## Formula: ~1 | Z
## Parameter estimates:
## 1 0
## 1.0000 0.9976
## Fixed effects: Yobs ~ 0 + Z + X + sid
## Value Std.Error DF t-value p-value
## Z 0.3701 0.06423 2086 5.762 0
## X 0.1837 0.00831 2086 22.108 0
## Correlation:
## Z
## X 0.002
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -3.519501 -0.670706 0.003627 0.626926 3.806052
##
## Number of Observations: 2117
## Number of Groups: 30Note that the above summary() throws a warning, as all of the site dummies have 0 degrees of freedom; just ignore that warning here.
Getting the empirical Bayes estimates by hand
You can also get the EB estimates by hand via coef() as follows:
site_ates = tibble( sid = rownames( coef(re.mod) ),
beta_hat = coef( re.mod )$Z )
print( site_ates, n=4 )## # A tibble: 30 × 2
## sid beta_hat
## <chr> <dbl>
## 1 1 0.456
## 2 2 0.323
## 3 3 0.432
## 4 4 0.0893
## # ℹ 26 more rowsAcknowledgements
Thanks to Kristen Hunter and Mike Weiss for edits and comments on this post.