A Matching Guide (Part 1 of 3: How do I make a matched dataset?)
by Thomas Leavitt and Luke MiratrixThis is a live document that is subject to updating at any time.
Introduction
This document, the first of a three part series, is an introduction to matching in R using the optmatch and RItools packages.
We focus on unit-to-unit matching, as opposed to other recent approaches that focus on obtaining overall balance in the distribution of the covariates across the sample by reweighting.
Focusing on unit matching specifically can take advantage of the intuition behind matching: if we match like with like, based on things before a treatment, then only random chance determined which units were assigned to treatment. Therefore, any differences in outcomes between treated and untreated units must be due to the existence of a treatment effect or random chance.
We introduce matching via an example that aims to infer the causal effect of United Nations (UN) peacekeeping interventions on the durability of post-conflict peace (Gilligan and Sergenti 2008), an important academic and policy question. We will use the optmatch package (see Hansen 2004, 2007; Hansen and Klopfer 2006), which makes use of the RELAX-IV optimization algorithm (Bertsekas and Tseng 1988; Bertsekas 1991, 1995, 1998) to construct matched strata that minimize the sum of covariate distances between each pair of treated and control units within each stratum. We also use RItools, the companion package that enables scholars to assess covariate balance and to perform outcome analysis once they have constructed matched strata (see Hansen and Bowers 2008).
In particular, the packages that we use are the following:
library("optmatch")
library("RItools")
library("haven")
library("tidyverse")Following Rosenbaum (2002, chap. 3), we can formally characterize a matched design as follows: There are \(n\) total units, \(n_C\) of which are in the control condition and \(n_T\) of which are in the treated condition. The process by which the control and treated units selected into their respective conditions is unknown, but we model it as a process where units individually get assigned to treatment or control via \(n\) (but not necessarily ) coin tosses. More specifically, we can write \(Pr( Z_i = z ) = \pi_i^{z} \left(1 - \pi_i\right)^{1 - z}, i = 1, \dots n\), where \(\pi_i \in (0, 1)\) for all \(i\).
For observational studies, we then assume “selection on observables,” which is that a \(\pi_i\) is solely a function of unit \(i\)’s observed baseline covariates, \(\mathbf{x}_i\). This means \(\pi_i\), i.e., \(\Pr\left(Z_i = 1\right)\) is equal to \(\lambda\left(\mathbf{x}_i\right)\), where \(\lambda\left(\cdot\right)\) is an unknown function. Even if we don’t know \(\lambda\left(\cdot\right)\), if \(\mathbf{x}_i = \mathbf{x}_j\) for any two units \(i\) and \(j \neq i\), then it follows that \(\lambda\left(\mathbf{x}_i\right) = \lambda\left(\mathbf{x}_j\right)\), i.e., \(\Pr\left(Z_i = 1\right) = \Pr\left(Z_j = 1\right)\). In other words, under this model, if two units have the same covariates, they also have the same chance of landing in the treatment group.
Of course, it is unlikely that two units \(i\) and \(j\) will be identical on all baseline covariates. But if the two units’ covariates are similar, then it remains plausible that \(\Pr\left(Z_i = 1\right) \approx \Pr\left(Z_j = 1\right)\) — i.e., their treatment assignment probabilities are approximately equal. This is the hope of matching.
When we match we construct blocks of treated and control units that are all similar on baseline covariates and, hence, have approximately equal probabilities of treatment assignment (under the assumption of no unobserved confounding). If units in a given block indeed have approximately equal treatment assignment probabilities, then it is just happenstance that, within a given block, our observed control units were the ones untreated and our observed treated units were the ones treated. We can thus treat that block as a miniature randomized experiment, and comparing the treated and control units within a given block will be a good one. Once we have our little mini-experiments, we aggregate them, analyzing our observational study as if it is a blocked and randomized experiment.1
So this is the idea behind matching. But how does one operationalize it? How do we navigate the various packages and pieces of software to do it in pratice? Providing answers to these questions is the goal of this tutorial. We give a high-level overview of some ideas behind matching, and also give code for implementing those ideas using various R packages. We also show some ways of doing a few of these things “by hand” to further underscore some of the conceptual issues, and to give more power to the practitioner for controlling the matching pipeline.
We break our UN interventions example (from Gilligan and Sergenti (2008)) into specific decision points that scholars will face, and present this overall pipeline in three main parts:
How do I measure unit similarity?
We use data from Gilligan and Sergenti (2008), which compares the duration of peace in post-conflict countries where the UN did (treated) and did not (control) intervene. We will make these comparisons within blocks that are similar on a range of baseline factors — such as the number of deaths and the duration of a country’s last war, the level of ethnic fractionalization and population size.
Gilligan and Sergenti (2008) use one-to-one (and later two-to-one) nearest neighbor matching with replacement via the GenMatch package in R (see Sekhon 2011).
After matching, Gilligan and Sergenti (2008) then estimate the average treatment effect on the treated (ATT) via a Cox proportional hazard model.
Our implementation of matching to follow differs from this approach and is not meant to be a replication of the findings from Gilligan and Sergenti (2008).
data <- read_dta("peace_pre_match.dta")Whether the UN intervened or not in a post-conflict country is the binary treatment variable (UN in the dataset) and the log duration (in months up to December 2003) of the post-conflict peace period is the outcome variable (dur in the dataset).
We ignore, here, issues of truncation of dur.
The other variables — e.g., population size (pop) and ethnic fractionalization (ethfrac) among others — are our baseline covariates.
Matching is about assessing similarity: we ask, ``how close was this country to this other country, before treatment?” This is usually operationalized with a distance measure assessing how different two units are. We then try to match units that are close.
We encode all the distances between units with a distance, or similarity, matrix, an \(n_T \times n_C\) matrix in which each row corresponds to each treated unit and each column corresponds to each control unit. Each cell is the distance between the corresponding treatment and control units, as measured by a distance statistic. That distance statistic is simply a function that maps the pair of the baseline covariates of a treated and control unit to a single number. The lower the number, the more similar the two units are.
There are many different distance metrics one could use. For example, we might compare post-conflict Liberia, where the UN did intervene, and post-conflict Guinea-Bissau, where they did not, using use the Euclidean distance on all their baseline covariates, as follows:
covs <- c("lwdeaths", "lwdurat", "ethfrac", "pop", "lmtnest", "milper",
"bwgdp", "bwplty2", "eeurop", "lamerica", "asia", "ssafrica", "nafrme")
liberia = data[data$cname == "Liberia", covs]
guinea_bissau = data[data$cname == "Guinea-Bissau", covs]
sqrt(sum(liberia - guinea_bissau)^2)[1] 57.77067We can get our entire matrix of these pairwise distance values with match_on() from the optmatch package:
## We have replaced the binary geographic region variables with one factor
## variable for region. The match_on will generate the binary indicators on the
## fly.
covs <- c("lwdeaths", "lwdurat", "ethfrac", "pop", "lmtnest", "milper",
"bwgdp", "bwplty2", "region")
cov_fmla <- reformulate(termlabels = covs, response = "UN")
dist_mat_euc <- match_on(x = cov_fmla,
data = data,
standardization.scale = NULL,
method = "euclidean")
## add names to matrix for readability
dimnames(dist_mat_euc) <- list(data$cname[data$UN == 1], data$cname[data$UN == 0])
dist_mat_euc[11:15, 27:30] Niger Guinea Togo Central African Republic
Sierra Leone 94.20754 101.17756 116.32355 116.94072
Zaire 26.67769 29.86983 45.62778 46.57041
Rwanda 66.75441 71.57247 77.03812 76.02807
Mozambique 133.46632 140.59774 155.39562 155.80475
Namibia 246.44441 253.23226 268.35491 268.08320In our little subset of the full distance matrix, above, the first entry is the distance of Sierra Leone (treated) from Niger (control). The last listed entry is the distance between Namibia (treated) and the Central African Republic (control).
One problem with Euclidean distance is that it is dependent on the scale of covariates — e.g., the difference between, say, a country in Africa (coded as 1 for the covariate ssafrica) and a country in Latin America (coded as 0 for the covariate ssafrica) yields the same Euclidean distance as the difference between one country with a per capita gross domestic product (GDP) of $3,000 and another with a per capita GDP of $3,001.
Roughly speaking, we want a difference in one variable to matter the same as a difference deemed to be similar in magnitude in another.
Another concern with Euclidian distance is it does not account for the correlation between multiple covariates.
A popular alternative distance measure is Mahalanobis distance (Mahalanobis 1936), which first standardizes the variables to put them on (hopefully) the same scale, and then (in effect) downweights correlated variables so they don’t get double counted. Construct a distance matrix using Mahalanobis distances instead of Euclidean distances as follows:
dist_mat_mah <- match_on(x = cov_fmla,
data = data,
standardization.scale = NULL,
method = "mahalanobis")Propensity scores as a measure of similarity
Another common choice is to calculate distance on the propensity score (the probability of landing in the treatment group). When there are many covariates, it is difficult to match directly on all of them. Propensity scores summarise this information into a single number, making matching more straightforward in principle. The intuition of why this works comes directly from the idea of matching: we want to form groups of units where all had the same chance of treatment. If we match on the chance of treatment, we have achieved this end. Matching on the propensity score is a two step process: (1) calculate the propensity scores, (2) use them as a covariate when calculating distances.
We first estimate the propensity score:
psm <- glm(formula = cov_fmla,
family = binomial(link = "logit"),
data = data)The linear predictors from the model psm above are the logit transformations of the model’s predicted probabilities, which are often easier to inspect and have better properties regarding distance for the more extreme ends. (This makes a propensity score of, say, 0.10 vs 0.05 much different than 0.50 and 0.55.)
p_score <- psm$linear.predictorsWe can assess the overlap between treatment and control units in their two empirical distributions of estimated propensity scores via the boxplot below. This boxplot might inform the choice of the calipers (see Althauser and Rubin 1970) we use for matching.
ggplot(data = data,
mapping = aes(x = as.factor(UN),
y = p_score)) +
geom_boxplot() +
xlab(label = "UN intervention") +
ylab(label = "Linear predicted probability") +
theme_bw() +
coord_flip()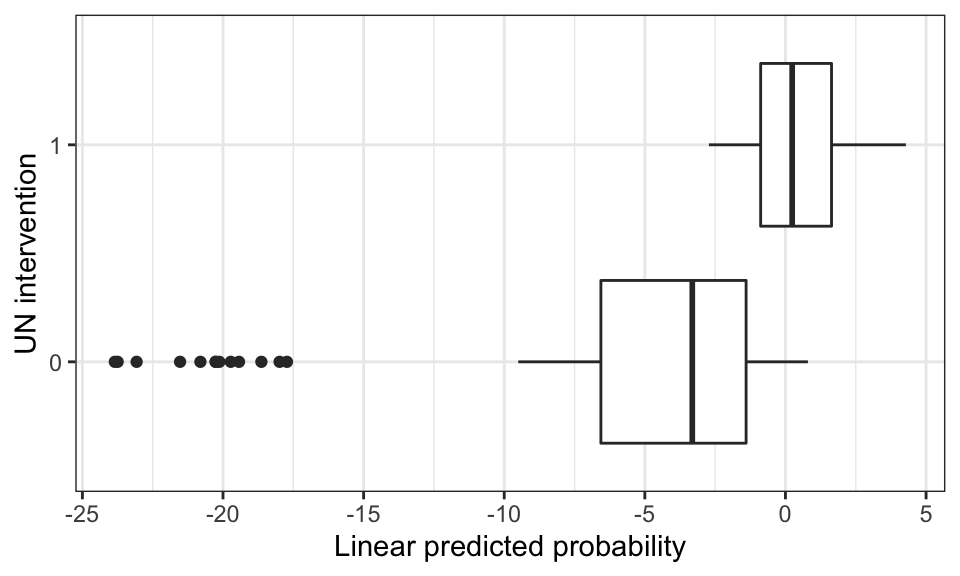
As the figure above shows, there is some, but not a lot of, overlap between our two groups. We can likely find some units that are similar for which we can construct matched sets. But we also see that most of the controls are not similar to any of the treated, and vice-versa.
How can I ensure that my matches will satisfy certain criteria?
When matching we may want to forbid matches that are “too poor,” preferring to simply drop units that have no viable counterpart. This is called “trimming.” This can be done in either of two primary ways: First, as a simpe example to build intuition, we will impose the following constraints:We ensure our matched sets satisfy these constraints by setting cell \(t,c\) in the distance matrix to \(\infty\) when treated country \(t\) and control country \(c\) do not satisfy our constraints.
Here we make our constraints:2
em_region <- exactMatch(x = UN ~ region,
data = data)
euc_dist_polity <- match_on(x = UN ~ bwplty2,
data = data,
standardization.scale = NULL,
method = "euclidean")
euc_dist_polity_cal_2 <- euc_dist_polity + caliper(x = euc_dist_polity,
width = 2)How do I actually match my units?
There are many, many ways of matching units that target different definitions of ``well matched.” We focus on individual match quality. In particular, we aim to divide our units into groups (blocks) with both treatment and control members such that the the sum of all the within-block covariate distances between treatment and control units is minimized. We do this with full matching. With full matching, each matched set will consist of one treatment unit and possibly many control units or one control unit and possibly many treatment units — a particular matched structure that Rosenbaum (1991) shows to be optimal.
The fullmatch() method solves an optimization problem to find the best possible matches:
em_region_fm_polity_cal_2 <- fullmatch(x = em_region + euc_dist_polity_cal_2,
data = data)
stratumStructure(em_region_fm_polity_cal_2)2:1 1:1 1:2 1:3 1:4 1:5 1:7 1:9 0:1
3 4 1 3 2 1 1 1 21 In the above call, we have our different components to our matching ``added” together.
As we can see from the output above, there are no treated countries that we were unable to match to at least one control country, but there are 21 control countries that we were unable to match to at least one treated country.
Who was matched to whom?
To figure out who was matched to whom, we need to dig into the results of the matching call. The matching call returns a list of categorical variables corresponding to the ``block IDs” for each country in our original data. We add it to the dataframe, and then we can tabulate:
data$fm_polity_cal <- em_region_fm_polity_cal_2
## Look at single block for illustration
filter(.data = data,
fm_polity_cal == "ssafrica.2") %>%
select(cname, UN, region, bwplty2 )# A tibble: 2 × 4
cname UN region bwplty2
<chr> <dbl> <chr> <dbl>
1 Niger 0 ssafrica -6
2 Sierra Leone 1 ssafrica -6Note how in the block we examined, the exact match on geographic region holds; all five countries in that block are in sub-Saharan Africa. The baseline Polity score is mostly the same, but not exact. In this matched set, the distance on the Polity score between the treated country (Sierra Leone) and each control country (Niger, Togo, Chad and Eritrea) is less than or equal to \(2\), which is exactly what we specified in our caliper on Polity score.3
What is the effective sample size?
Because our blocks have different numbers of treated and control units, we will have to reweight some units to balance out others. For example, in a block with 1 treatment and 2 control units, each control unit would be weighted as 1/2 as they together are a match for the treated unit. This means that our effective sample size, i.e., how much information we have in our dataset, may be different than the actual (consider a block with 1 treated and 1000 control units: even though we know the control side very well, we only have a single unit to estimate the treatment side).
To calculate effective sample size, we use a function like so:
effectiveSampleSize(em_region_fm_polity_cal_2)[1] 22.25ns <- data %>% group_by( fm_polity_cal ) %>%
summarise( nT = sum( UN == 1 ),
nC = sum( UN == 0 ) )
sum( 2 / (1/ns$nT + 1/ns$nC) )[1] 22.25The reported effective sample size of \(22.25\) refers to the sum across blocks of the within-block harmonic mean of the number of treated and control subjects — that is, \(\sum \limits_{b = 1}^B \left[\left(n_{bT}^{-1} + n_{bC}^{-1}\right)/2\right]^{-1}\), where the index \(b\) runs over the \(\left\{1, \dots , B\right\}\) blocks, \(n_{bT}\) is the number of treated units in block \(b\), \(n_{bC}\) is the number of control units in block \(b\), \(n_b\) is the number of total units in block \(b\) and \(n = \sum \limits_{b = 1}^B n_b\) now denotes the total number of units in the entire study.
How do I relax my matching to get more units matched?
We might be concerned that our effective sample size is too low. Let’s say that we want to maintain exact balance on geographic region. But perhaps we could increase the caliper on Polity score such that countries who are more than two points apart from each other are allowed to be in the same matched set. Would increasing the caliper to 3 increase our effective sample size (ideally without inducing too much imbalance on Polity)? We can directly assess whether this is true.
euc_dist_polity_cal_3 <- euc_dist_polity + caliper(x = euc_dist_polity,
width = 3)
em_region_fm_polity_cal_3 <- fullmatch(x = em_region + euc_dist_polity_cal_3,
data = data)
stratumStructure(em_region_fm_polity_cal_3) 2:1 1:1 1:2 1:3 1:4 1:5 1:7 1:10 0:1
3 2 1 3 3 2 1 1 13 effectiveSampleSize(em_region_fm_polity_cal_3)[1] 23.53485We have matched 8 additional controls, leaving only 13 control countries unmatched as compared to 21 when we used a caliper of 2 on Polity score. Even though we now have 8 more countries in our study, the effective sample size increases by only \(\approx 1.3\). Why is this? The reason is the bulk of our control units were added to only two of our blocks. Since these blocks still have only a single treated unit, the precision of the impact estimate for those blocks is not substantially enhanced. In other words, the extra control units give us more precision in areas where it is less useful. In general, we would ideally want roughly even splits of treatment and control across our blocks. Unfortunately, when we are more loose with matching, we will mainly pick up units “on the fringe,” and they will often cluster, frequently getting matched to the same comparisons.
Here we compare the distribution of blocks under the two caliper settings. Note the reduction of 1:1 blocks and increase of 1:4 and 1:5 blocks:
stratumStructure(em_region_fm_polity_cal_2)2:1 1:1 1:2 1:3 1:4 1:5 1:7 1:9 0:1
3 4 1 3 2 1 1 1 21 stratumStructure(em_region_fm_polity_cal_3) 2:1 1:1 1:2 1:3 1:4 1:5 1:7 1:10 0:1
3 2 1 3 3 2 1 1 13 Mahalanobis distance and propensity score matching
The simple form of matching above (based on an exact match on geographic region and Euclidean distance on one covariate, Polity score) helps to illustrate ideas. To match on many covariates, we will likely want to use some combination of Mahalanobis distance and propensity score matching. In what follows, we will match on rank-based Mahalanobis distance, the benefits of which are explained in Rosenbaum (2010), within a caliper on the propensity score and the restriction that treated and control countries must belong to the same geographic region.
We will use a caliper of \(0.25\) on the propensity score.4 The choice of caliper often reflects a back-and-forth process between optimizing effective sample size subject to satisfying some pre-determined balance constraint. In this case, we sought to have as large of an effective sample size as possible subject to having an omnibus \(p\)-value from a test of overall covariate balance (see Hansen and Bowers 2008, 11–12) greater than or equal to \(0.65\) (to be discussed below).
data$p_score <- psm$linear.predictors
ps_dist_mat <- match_on(x = UN ~ p_score, data = data)
ps_dist_cal <- ps_dist_mat + caliper(x = ps_dist_mat,
width = 0.25)
dist_mat_rank_mah <- match_on(x = UN ~ lwdeaths + lwdurat + ethfrac + pop +
lmtnest + milper + bwgdp + bwplty2,
data = data,
method = "rank_mahalanobis")
fm <- fullmatch(x = dist_mat_rank_mah + ps_dist_cal + em_region,
data = data)
summary(fm)Structure of matched sets:
1:0 1:1 1:2 1:3 1:4 1:5+ 0:1
5 8 2 1 1 2 36
Effective Sample Size: 17.2
(equivalent number of matched pairs).data$fm <- fmAfter I have constructed matched sets, how do I know if I have matched well enough?
Once we have constructed our matched sets, we want to assess covariate balance and, in particular, to assess whether covariate balance in our matched observational study compares favorably with the covariate balance we might have observed in an actual block randomized experiment. One way to assess covariate balance after matching is via the approach laid out in Hansen and Bowers (2008):
cov_bal <- xBalance(fmla = UN ~ lwdeaths + lwdurat + ethfrac + pop +
lmtnest + milper + bwgdp + bwplty2 + region,
strata = list(unstrat = NULL,
fm = ~ fm),
data = data,
report = c("adj.means", "std.diffs"))
#kable( cov_bal, digits = 2 )The balance table shows that balance in covariate means after matching is much better than before matching.
The omnibus \(\chi^2\) covariate balance test statistic, which assesses balance on all covariates and their linear combinations (see Hansen and Bowers 2008, 11–12), yields a \(\chi^2\) test statistic of \(5.97\) and a \(p\)-value of roughly \(0.65030\).
xBalance(fmla = UN ~ lwdeaths + lwdurat + ethfrac + pop +
lmtnest + milper + bwgdp + bwplty2 + region,
strata = list(unstrat = NULL,
fm = ~ fm),
data = data,
report = "chisquare.test")---Overall Test---
chisquare df p.value
unstrat 29.2 12 0.00367
fm 6.0 8 0.64677A high \(p\)-value in this case means that our level of covariate balance is consistent with what we would observe in a uniform, block randomized experiment. Of course, it is still difficult to tell if this level of covariate balance is sufficient. Our study may still suffer from bias due to residual (after matching) imbalances on observed covariates, as well as imbalances on unobserved covariates. For now we will proceed as if our matched study does not suffer from bias, but we will subsequently assess the sensitivity of our inferences to residual imbalances on observed covariates and unobserved covariates.
Conclusion
We now have a matched dataset. Ideally, our final collection of treated and control units are comparible. We hope that, for these units, it was just happenstance which “got treated” and which did not. In our next part we will treat these data as a blocked randomized experiment to estimate the impact of treatment.
References
For more on the analysis of blocked experiments, see Gerber and Green (2012).↩︎
Note we are using Euclidean distance. This is because, in this case, we are exactly matching on geographic region and only have a single variable, Polity score, left over so we do not have to worry about the relative scales of variables.↩︎
Note that the distance on Polity score between the control countries could potentially be greater than \(2\), but we are concerned only with the distance between the treated country and each control country.↩︎
This more or less accords with the rough guideline from Cochran and Rubin (1973) and Rosenbaum and Rubin (1984) for a caliper of \(0.2\) on the propensity score.↩︎